Materi Pertemuan 2

 GARIS SINGGUNG LINGKARAN

Sebelum menentukan persamaan garis singgung lingkaran, ada baiknya kita mengingat kembali mengenai sifat-sifat garis singgung lingkaran. Garis singgung lingkaran merupakan garis yang menyinggung suatu lingkaran. Kata kunci dari definisi tersebut adalah “menyinggung”. Apabila suatu garis menyinggung lingkaran, maka garis tersebut tepat melalui satu titik pada lingkaran. Perhatikan beberapa kedudukan garis terhadap lingkaran berikut.



Berdasarkan gambar di atas, kita dapat melihat bahwa garis k tidak memotong lingkaran O, garis l menyinggung lingkaran O di titik A, dan garis m memotong lingkaran O di titik-titik B dan C. Karena suatu garis singgung tepat melalui satu titik pada lingkaran (misalkan titik A), maka garis singgung tersebut akan tegak lurus dengan jari-jari lingkaran yang menghubungkan titik A dengan titik pusat lingkaran. Sifat dari garis singgung tersebut dapat digunakan untuk menentukan persamaan garis singgung lingkaran.

1. Menentukan Persamaan Garis Singgung Lingkaran
Pada bagian ini kita akan menentukan persamaan garis singgung yang melalui titik A(x₁, y₁) pada lingkaran yang memiliki persamaan x² + y² = r², yaitu lingkaran yang berpusat di titik (0, 0) dan berjari-jari r. Perhatikan ilustrasi berikut.





Misalkan kita akan menentukan persamaan garis g yang melalui titik A(x₁, y₁), yaitu titik pada lingkaran x² + y² = r². Karena titik A(x₁, y₁) terletak pada lingkaran x² + y² = r² maka,

Selanjutnya kita buat ruas garis OA, yaitu ruas garis yang memiliki ujung-ujung di titik O (pusat lingkaran) dan titik A. Sehingga gradien dari ruas garis tersebut adalah

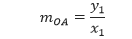
Karena garis g tegak lurus dengan ruas garis OA, maka

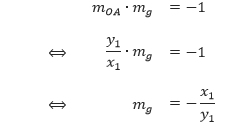
Karena garis g melalui titik A(x₁, y₁) dan bergradien m_g = –x₁/y₁, maka persamaan garis g dapat ditentukan sebagai berikut.

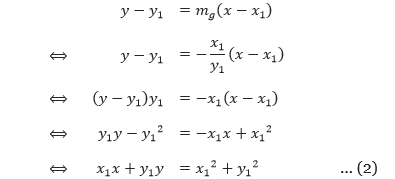
Dengan mensubstitusi persamaan (1) ke persamaan (2) diperoleh x₁x + y₁y = r². Sehingga, persamaan garis singgung yang melalui satu titik pada lingkaran x² + y² = r² dapat disimpulkan sebagai berikut.

Persamaan Garis Singgung Lingkaran
Persamaan garis singgung yang melalui titik A(x₁, y₁) pada lingkaran x² + y² = r² adalah x₁x + y₁y = r².

Untuk lebih memahami mengenai persamaan garis singgung lingkaran, perhatikan contoh berikut.
Contoh: Menentukan Persamaan Garis Singgung
Tentukan persamaan garis singgung yang melalui titik (2, –3) pada lingkaran x² + y² = 13.
Pembahasan Dengan (x₁, y₁) = =(2, –3) dan x² + y² = 13, kita mendapatkan x₁ = 2, y₁ = –3, dan r² = 13. Sehingga persamaan garis singgung tersebut adalah

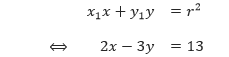
2. Sifat-sifat garis singgung lingkaran

a) Garis singgung lingkaran tegak lurus pada diameter lingkaran yang melalui titik singgungnya.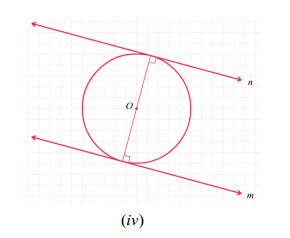


b) Melalui suatu titik pada lingkaran hanya dapat dibuat satu dan hanya satu garis singgung pada lingkaran tersebut.

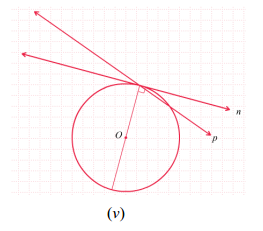
Garis p bukan garis singgung lingkaran O. Garis n merupakan garis singgung lingkaran O .

c) Melalui suatu titik di luar lingkaran dapat dibuat dua garis singgung pada lingkaran tersebut.


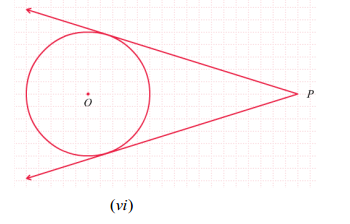
d) Jika P di luar lingkaran maka jarak P ke titik-titik singgungnya adalah sama.

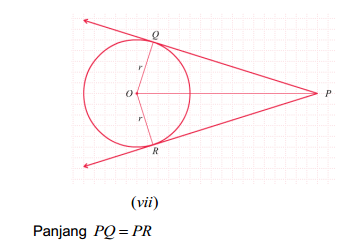
3. Menentukan panjang garis singgung dari suatu titik di luar lingkaran

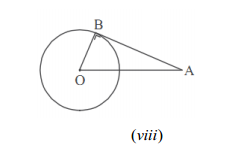
AB adalah garis singgung lingkaran O , AB tegaklurus OB , OB adalah jari-jari lingkaran. Panjang AB ditentukan dengan menggunakan dalil Pythagoras.

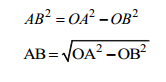
Contoh Soal :

Diketahui sebuah lingkaran dengan pusat di O dan panjang jari-jari 7cm. Garis AB adalah garis singgung lingkaran yang ditarik dari titik A di luar lingkaran. Jika panjang OA 15cm , panjang AB ...cm

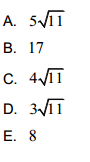
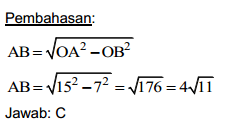
3. Garis Singgung Persekutuan Dua Lingkaran

a. Garis Singgung Persekutuan Dalam Dua Lingkaran

Diketahui dua lingkaran L1 dan L2 berpusat di P dan Q, dan panjang jari-jari R dan r.

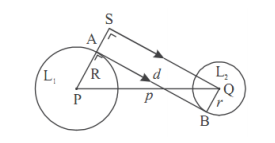
AB adalah garis singgung persekutuan dalam dua lingkaran L1 dan L2. Panjang PQ = p , panjang AB = d.

Cara menentukan panjang AB sebagai berikut.
- Buatlah garis SQ yang sejajar AB dan sama panjang, sehingga terbentuk segitiga siku-siku PQS .
- Panjang AB SQ , tetapkan panjang SQ dengan dalil Pythagoras.


Contoh:
Dua lingkaran dengan panjang jari-jari 7 cm dan 3 cm, jarak antara dua titik pusat adalah 26 cm. Panjang garis singgung persekutuan dalam adalah … cm.
A. 24
B. 20
C. 18
D. 16
E. 12

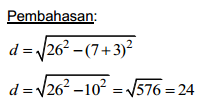
Jadi, Panjang garis singgung persekutuan dalam adalah 24 cm.
Jawab : A

b. Garis Singgung Persekutuan Luar Dua Lingkaran

Diketahui dua lingkaran L1dan L2 berpusat di P dan Q, dan panjang jari-jari R dan r .

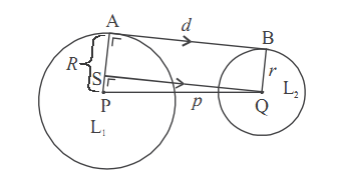
AB adalah garis singgung persekutuan luar dua lingkaran L1 dan L2. Panjang PQ = p, panjang AB = d.
Cara menentukan panjang AB sebagai berikut :
- Buatlah garis SQ yang sejajar AB dan sama panjang, sehingga terbentuk segitiga siku-siku PQS.
- Panjang AB = SQ, tetapkan panjang SQ dengan dalil Pythagoras


Contoh:
Dua lingkaran dengan panjang jari-jari 8 cm dan 3 cm, jarak antara dua titik pusat
adalah 13 cm. Panjang garis singgung persekutuan luar adalah … cm.
A. 15
B. 12
C. 10
D. 9
E. 7

Materi pertemuan 1

  LINGKARAN

Siapa yang tidak tahu ban mobil dan uang logam? Itu merupakan barang-barang yang mudah Anda temui dalam kehidupan sehari-hari. 

Ban mobil dan uang logam merupakan contoh benda-benda yang memiliki bentuk dasar lingkaran. Secara geometris, benda-benda tersebut dapat digambarkan seperti pada Gambar (a).

Perhatikan Gambar (b) dengan saksama. Misalkan A, B, C merupakan tiga titik sebarang pada lingkaran yang berpusat di O. Dapat dilihat bahwa ketiga titik tersebut memiliki jarak yang sama terhadap titik O. Dengan demikian, lingkaran adalah kumpulan titik-titik yang membentuk lengkungan tertutup, di mana titik-titik pada lengkungan tersebut berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut sebagai titik pusat lingkaran. Pada Gambar (b) , jarak OA, OB, dan OC disebut jari-jari lingkaran.
Jadi dapat disimpulkan bahwa lingkaran adalah kurva tertutup sederhana yang merupakan tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu. Jarak yang sama tersebut disebut jari-jari lingkaran dan titik tertentu disebut pusat lingkaran. Garis lengkung tersebut kedua ujungnya saling bertemu membentuk keliling lingkaran dan daerah lingkaran (luas lingkaran).

Rumus keliling dan luas lingkaran sebenarnya sudah diajarkan sejak kita masih duduk di bangku sekolah dasar. Namun saya akui memang rumus yang satu ini memang yang paling sering terlupakan oleh saya dan mungkin juga anda. Entah kenapa mungkin karena rumus ini memang jarang saya gunakan mungkin ya, hehe.

Pada dasarnya antara rumus keliling dan luas lingkaran memang hampir mirip jika diperhatikan sekilas saja. Terkadang malah membuat kita sering terbalik memahami mana yang merupakan rumus kelilingnya dan mana yang merupakan rumus luasnya. Hal ini sering dialami oleh kebanyakan orang jika mereka tidak memperhatikan rumusnya secara seksama, mungkin anda juga begitu?

Baiklah mari kita mulai pembahasan kita pada kali ini. Pembahsan akan saya mulai dari rumus keliling lingkaran.

Rumus Keliling Lingkaran

Rumus umumnya yaitu

Keliling = π x d
Denan keterangan sebagai berikut :
π = phi = 3,14 atau 22/7
d = diameter

Dikarenakan diameter (d) = 2 kali jari-jari (r) maka rumusnya bisa juga menjadi seperti berikut :

Keliling = π x 2 r
Atau biasa kita gunakan
Keliling = 2 π r

Baik, mari kita lanjut pada pembahasan rumus luasnya.

Rumus Luas Lingkaran

Luas = π r²
Dengan keterangan sebagai berikut :
π = phi = 3,14 atau 22/7
r = jari-jari lingkaran

Contoh soal :

1. Diketahui sebuah roda memiliki diameter 28 cm. Tentukan luas dan kelilingnya.
Pembahasan
Karena soal ini sangat jelas untuk dikerjakan maka anda tinggal memasukkan saja diameternya kedalam rumus luas dan kelilingnya.
Luas = π r²
Luas = 22/7 x 14 cm x 14 cm
Luas = 616 cm²
Nah lanjut mencari kelilingnya.
Keliling = 2 π r
Keliling = 2 x 22/7 x 14 cm
Keliling = 88 cm.
2. Andi ingin membuat sebuah gerobak. Dia membutuhkan setidaknya 4 roda agar gerobak itu bisa berjalan dengan sempurna. Total keliling keempat rodanya adalah 264 cm. Hitunglah berapa diameter masing-masing roda tersebut.
Pembahasan
Diketahui bahwa gerobak tersebut memiliki 4 roda.
Total keliling keempat rodanya adalah 264 cm.
Nah yang harus kita lakukan pertama kali ialah mencari total keempat diameternya dulu.
Keliling = π d
264 cm = 22/7 x d
22/7 x d = 264 cm,
diameter keempat roda = 84 cm
Diameter masing-masing roda = 1764/4
Diameter masing-masing roda = 21 cm